Networks
Analysis of structure
Motivation
Ecological networks offer a powerful approach to comprehensively analyze entire systems comprising hundreds of species and their thousands of interactions. There are almost infinite ways in which hundreds of species can possibly interact. Networks allow to determine the specific, non-random interaction structure that actually occur in nature of those almost infinite possibilities. These networks also allow the study of the interplay between structure and dynamics of complex systems of interacting species, shedding light on how this interplay influences system responses to perturbations.
Overview
Required R-packages
# PACKAGE LIST:
Packages <- c("tidyverse",
"kableExtra",
"bipartite")
# (INSTALL AND) LOAD PACKAGES:
# install.packages(Packages, dependencies = TRUE)
lapply(Packages, library, character.only = TRUE)
Exercise code and data
In addition to the in-text links below, you can download what you’ll need in this GoogleFolder.
Terminology
A network consists of nodes and edges, where nodes represent discrete entities like people, computers, cities, or species, and edges (or links) represent the connections between these entities. Networks can be weighted or unweighted, depending on whether the connections have associated values or not. In weighted networks, the edges have numerical values that indicate the strength or distance of the connection between nodes. In the case of plant-pollinator networks, that weight has traditionally been the number or fraction of visits or pollen transported.
Networks can also be directed or undirected. In directed networks, such as food webs, the connections between nodes have a specific direction, such as the flow of energy, indicating a one-way relationship. In undirected networks, such as mutualistic networks, the connections are bidirectional, showing a two-way relationship between nodes (i.e., reciprocal benefits). We will see later that the reciprocal benefits between plant and pollinator species can be decomposed into the mechanisms by which those benefits are provided, which can convert the bidirectional links between species into two unidirectional links (i.e., consumption of floral rewards and pollination services).
Networks can also be unipartite or bipartite. Unipartite networks such as food webs consist of a single set of nodes (species), where edges can connect any pair of nodes within that set (any species can potentially be eaten by others). On the other hand, nodes in bipartite networks are divided into two disjoint sets, such as plants and pollinators, and edges (representing which pollinator species visits which plant species) only connect nodes from different sets (e.g., plants cannot visit other plants).
Below, there is an illustration of a plant-pollinator system represented as a bipartite network, with three plant and three pollinator species.
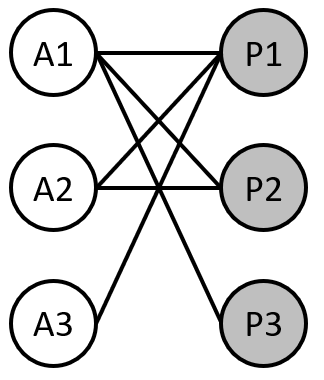
Ecological networks can be represented in various ways including a graph (as shown in the image above) or a matrix. Being able to switch between graph (network) and matrix form is powerful for understanding the full suite of network metrics we will see later.
Exercise 1
Using the bipartite network graph above, draw the corresponding matrix for the network. Assume that matrix columns represent animal species while matrix rows represent plant species. In the matrix cells, use 1’s to indicate an interaction between that animal and plant species and 0’s or blanks to indicate no interaction between species.
Network data
This workshop is focused on the integration of empirical data and theory in pollination networks. An important first step toward that integration is to know how to take empirical data and convert them into the standardized matrix format that is used in most packages and functions. For mutualistic networks like plant-pollinator networks, as discussed above, that format is a bipartite matrix with plants as rows, pollinators as columns, and (typically) counts of interactions filling the matrix.
Typically, empirical data collected on ecological networks take the form of an edge list. This is the case for pollination networks in particular. To collect pollination network data, we are typically observing a set of flowers. When a flower visitor (presumed pollinator) visits a plant, we would record on a data sheet or field notebook the identity of the plant species and the identity of the flower visitor species. (In the field, we might capture an insect pollinator for later identification, but the idea remains the same, that at some point we would have a data sheet with the identities of the plants and the pollinators).
Similarly, you could also have an edge list created through pollen DNA metabarcoding; while you might need to play around with the formatting a bit it is common to end up with an edge list like you would have from field data collection.
That might look something like this:
| id.num | plant | pollinator |
|---|---|---|
| 2371 | Delphinium barbeyi | Bombus flavifrons |
| 2372 | Heracleum spondophyllum | Thricops sp. |
| 2373 | Mertensia fusiformis | Bombus flavifrons |
| 2374 | Delphinium barbeyi | Bombus appositus |
| 2375 | Delphinium barbeyi | Bombus flavifrons |
| 2376 | Mertensia fusiformis | Colias sp. |
| 2377 | Delphinium barbeyi | Bombus flavifrons |
… but we want to turn that into a bipartite matrix.
One approach for coding that transformation is in the code chunk below, focused on the tidyverse way of doing things.
The general approach is:
- group our data by plant species and pollinator species
- tally the number of visits for each pollinator species that plant species—basically “collapsing” the rows that have the same plant-pollinator combinations and counting up how many interactions there were for each unique plant-pollinator combination
- keeping the plants as rows, use the
pivot_widerfunction indplyr(part of thetidyverse) to create a new column for each pollinator species, filling in for each plant-pollinator combination the number of interactions we calculated in the prior step- in doing this step, we are also “collapsing” all of the plant rows such that there will be one row per plant
Let’s see this in action. We’ll start with the data frame called edgelist which is exactly the same as the data in the table above.
For the first two steps, here is how we do that, and what it looks like:
# step 1:
weighted <- edgelist %>%
group_by(plant, pollinator) %>%
# step 2:
tally()
# show in nicely-formatted table:
kable(weighted, row.names = FALSE) %>%
kable_styling(
full_width = FALSE,
position = "left",
bootstrap_options = "condensed"
)
| plant | pollinator | n |
|---|---|---|
| Delphinium barbeyi | Bombus appositus | 1 |
| Delphinium barbeyi | Bombus flavifrons | 3 |
| Heracleum spondophyllum | Thricops sp. | 1 |
| Mertensia fusiformis | Bombus flavifrons | 1 |
| Mertensia fusiformis | Colias sp. | 1 |
the new weighted dataframe is displayed above.
You’ll see that it created a new column called “n” that contains the tallied the number of times each unique interaction occurred.
It also “collapsed” the rows into unique plant-pollinator interactions;
previously there were 7 rows, and now there are 5, because one of the unique interactions (between Bombus flavifrons and Delphinium barbeyi) happened three times.
Moving from this, let’s check out the next step, where where using the pivot_wider function we pivot the single “pollinator” column to form one new column for each unique entry in the old column.
We will fill in the values for each row-by-column combination from the tallied interactions (the new “n” column).
Again there are 5 rows in this new matrix, with 4 unique values (Bombus flavifrons is represented twice), so we expect to see four pollinator columns emerge in the next step.
Similarly, this should collapse the 5 current plant rows into 3, one for each unique plant species. So we should see a 3 row \(\times\) 4 column bipartite matrix when we are done.
This is how to get there:
bipart.net <- weighted %>%
pivot_wider(id_cols = c("plant"), # plants are the rows
names_from = pollinator, # names of new columns: unique pollinators
values_from = n, # values in the matrix from tallied interactions
values_fill = 0) # if no value, enter zero (otherwise NA)
# show in nicely-formatted table:
kable(bipart.net, row.names = FALSE) %>%
kable_styling(full_width = FALSE,
position = "left",
bootstrap_options = "condensed")
| plant | Bombus appositus | Bombus flavifrons | Thricops sp. | Colias sp. |
|---|---|---|---|---|
| Delphinium barbeyi | 1 | 3 | 0 | 0 |
| Heracleum spondophyllum | 0 | 0 | 1 | 0 |
| Mertensia fusiformis | 0 | 1 | 0 | 1 |
looks just as hoped for: a 3-row by 4-column matrix. Note in the code above that we specified that values_fill = 0.
We did this because otherwise R would not know how to fill in the combinations for which it doesn’t have any information, and so it would fill them in with NA if we left that argument out.
Exercise 2
Edge List to bipartite network
Let’s practice turning an edge list into a bipartite network; this time we will do it at a (slightly) larger scale. We are going to use data collected by Berry’s Community Ecology class at the University of Washington in spring 2022, at the UW Medicinal Plant Garden (just outside the Life Sciences Building, where the Brosi Lab is based). The data for pollinators were collected at the family level.
Download the data file: medgarden.csv.
Import it and follow the steps above to generate a bipartite network. Call the resulting dataframe bipartite.med.
You should get this bipartite network back:
| plant | Osmia | Bombus | Syrphid | Halictid | Muscid | Ant | Hummingbird |
|---|---|---|---|---|---|---|---|
| Borago officinalis | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Camassia leichtlinii | 0 | 1 | 2 | 0 | 0 | 0 | 0 |
| Catharanthus roseus | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Coclearia afficinalis | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| Eriogonum umbellatum | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
| Erysimum asperum | 0 | 0 | 4 | 1 | 0 | 2 | 0 |
| Gilia capitata | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| Glaucium flavum | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Helleborus orientalis | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Heuchera micrantha | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| Heuchera sanguinea | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Horminum pyrenaicum | 0 | 0 | 3 | 0 | 0 | 0 | 0 |
| Hydrophyllum virginiana | 0 | 0 | 4 | 0 | 1 | 0 | 0 |
| Iris douglasiana | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Polemonium reptans | 3 | 0 | 0 | 0 | 2 | 0 | 0 |
| Polygonum bisorta | 0 | 0 | 0 | 3 | 1 | 0 | 0 |
| Rhodiola rosea | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Ruta graveolens | 0 | 0 | 0 | 2 | 0 | 0 | 0 |
| Sedua spathulifolium | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| Smilacina stellata | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Thymus leucospermus | 1 | 0 | 1 | 2 | 0 | 0 | 0 |
| Tragopogon porrifolius | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Wyethia angustifolia | 1 | 6 | 2 | 0 | 0 | 0 | 0 |
Data formatting
We have successfully achieved our objective of converting our edge list to a bipartite network. Still, if we want to use those data with the bipartite package we will need to do a little bit of extra formatting, as bipartite expects the data in matrix form (not a tibble or dataframe) and with the plant names as row names, not a separate column (matrices in R can only contain numeric values). Here is one way to do that (there are certainly more concise ways to code this):
# save plant names
plant = bipart.med$plant
# remove plant column
bipart.med = bipart.med[,-1]
# convert to matrix
bipart.med = as.matrix(bipart.med)
# add plants to row names
row.names(bipart.med) = plant
# remove `plant` variable (just to keep workspace clean)
rm(plant)
Visualization
At the beginning of our materials we covered the two basic ways of visualizing networks, through network diagrams (which show links as lines between nodes) and in matrix format (where each node is a row and/or a column). While understanding those two basic formats is foundationally important for working with networks, visualization is a large and complex topic. Here, in the interest of time, we will cover only one additional facet: how to standardize matrix depictions of networks, with a focus on bipartite networks.
Matrix depictions
What is the difference between these two matrices?
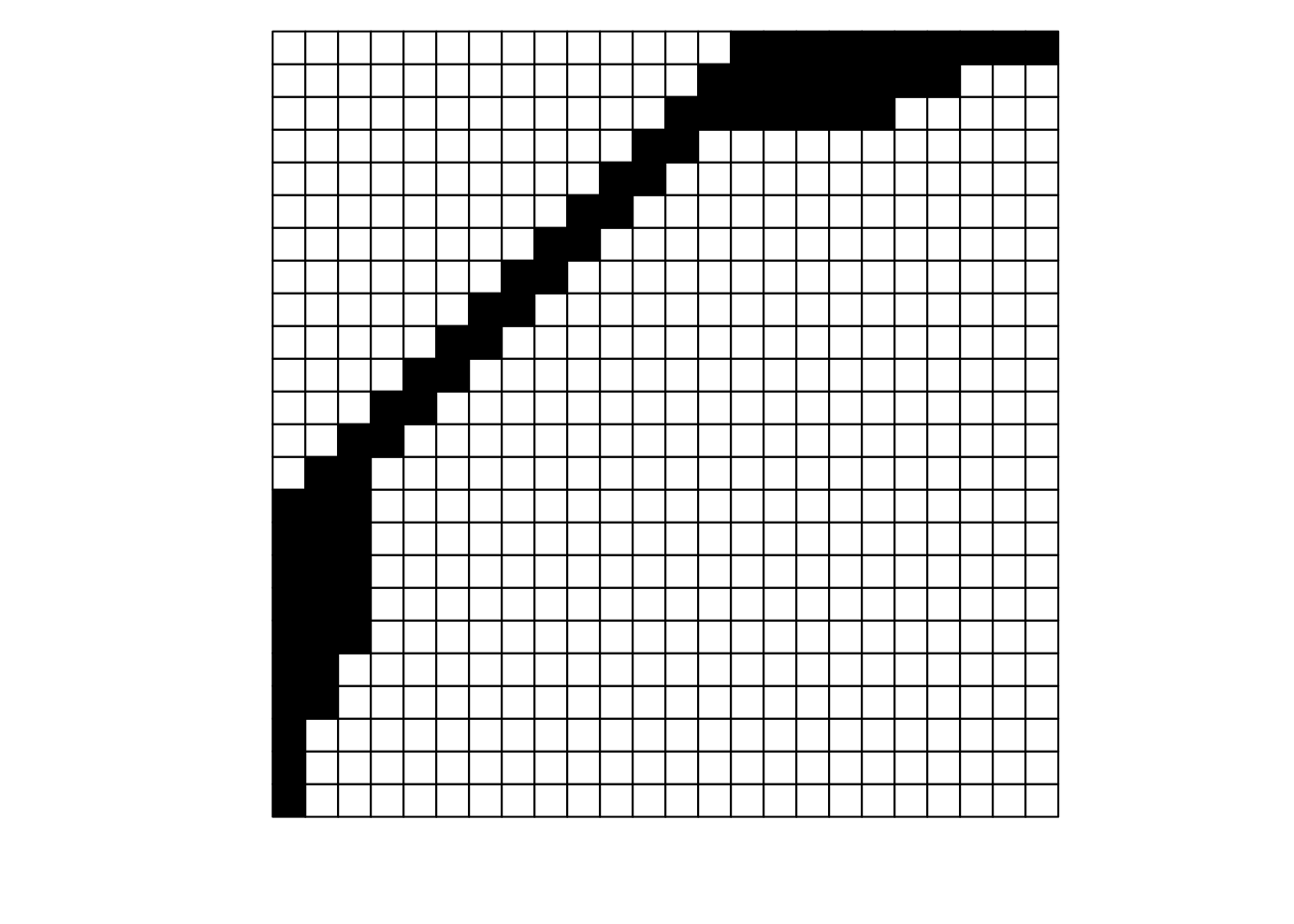
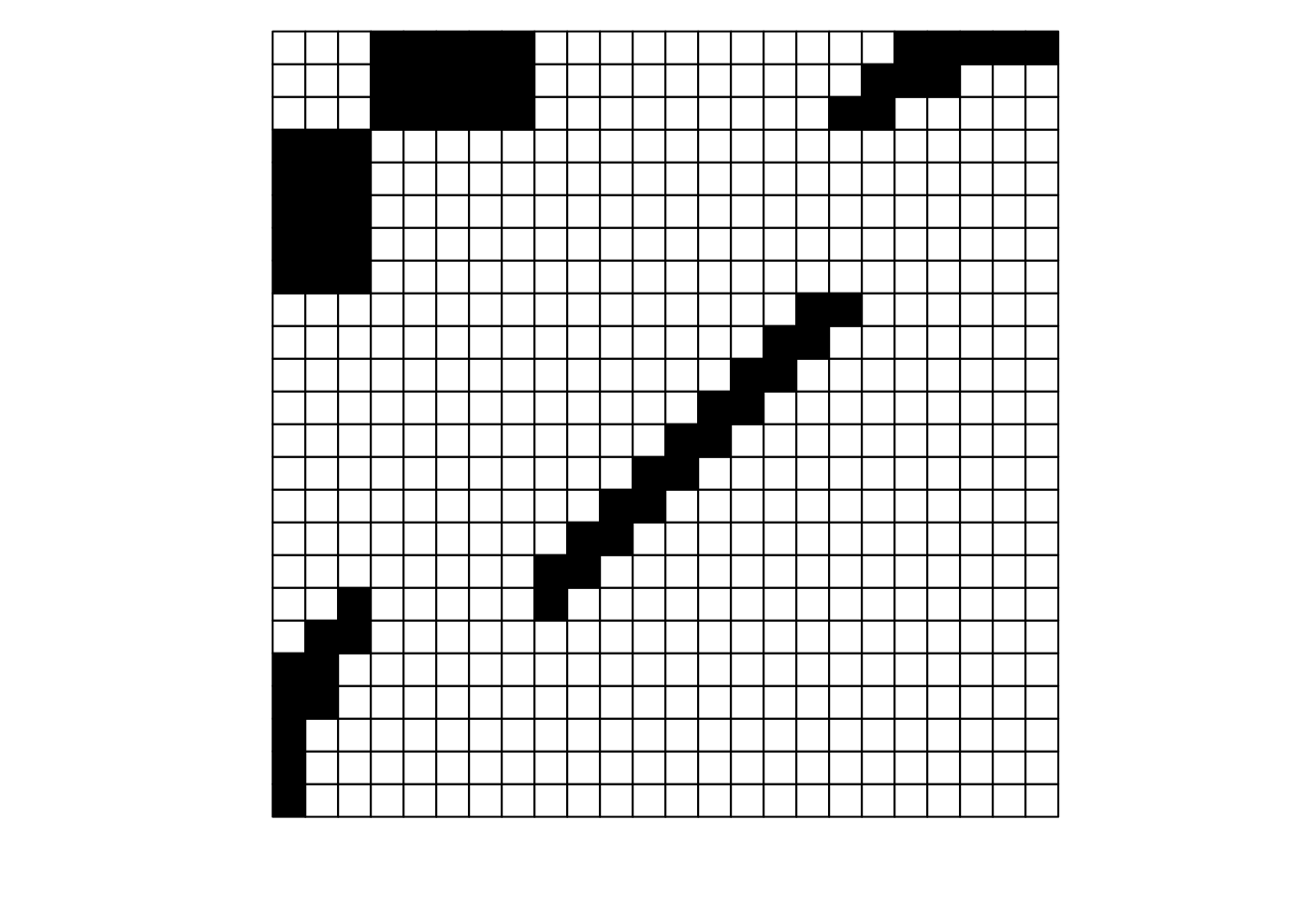
They look pretty different, huh? The second one gives off some distressed Jack-O-Lantern vibes…
Perhaps surprisingly, these are two different visualizations of the exact same network! How can that be?
Ultimately, as long as each interaction is recorded faithfully, we can move around the order of entire rows and entire columns and it is still the same network. If we re-plot the two figures above, including the row and column labels, we can perhaps see that more easily:
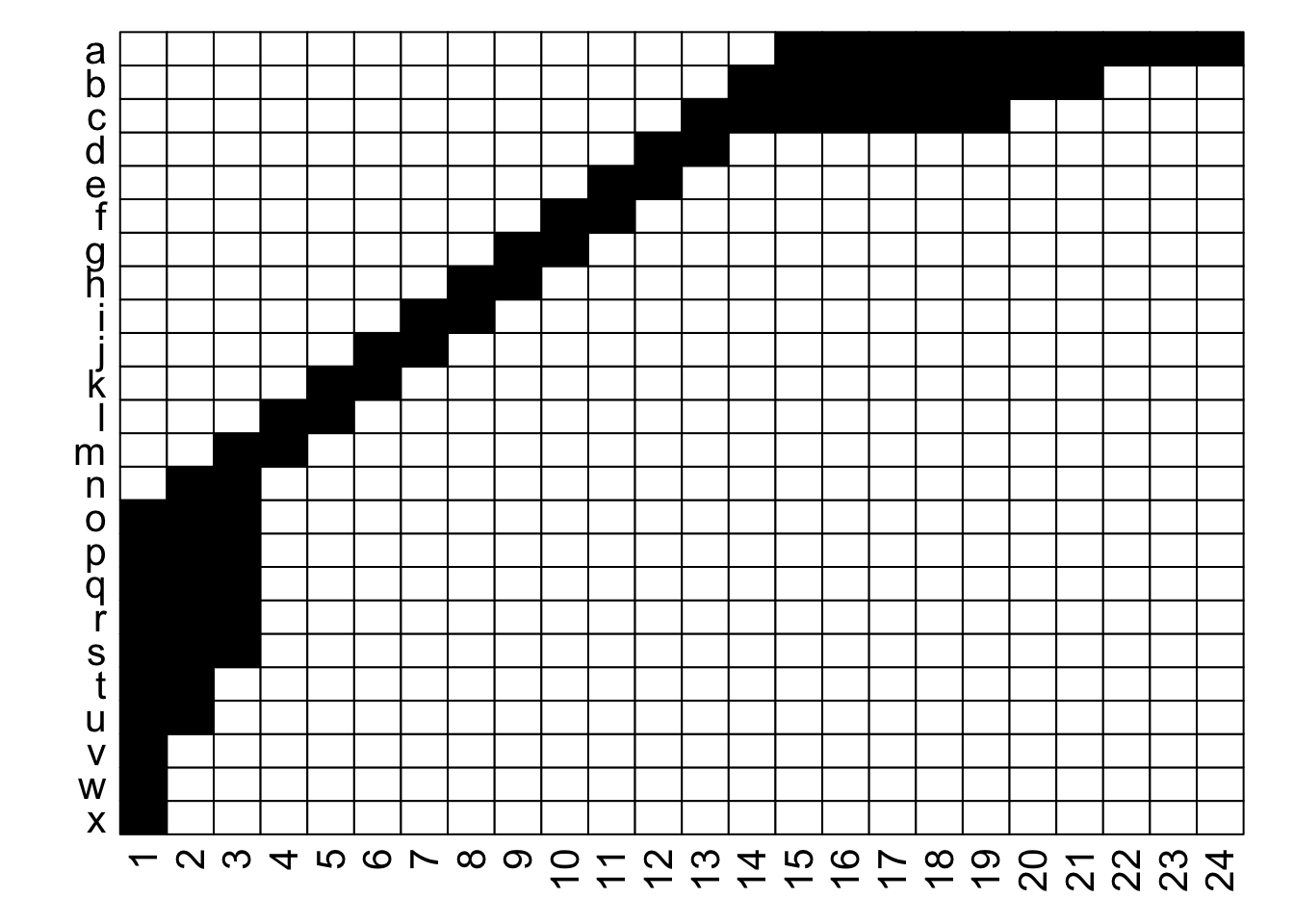
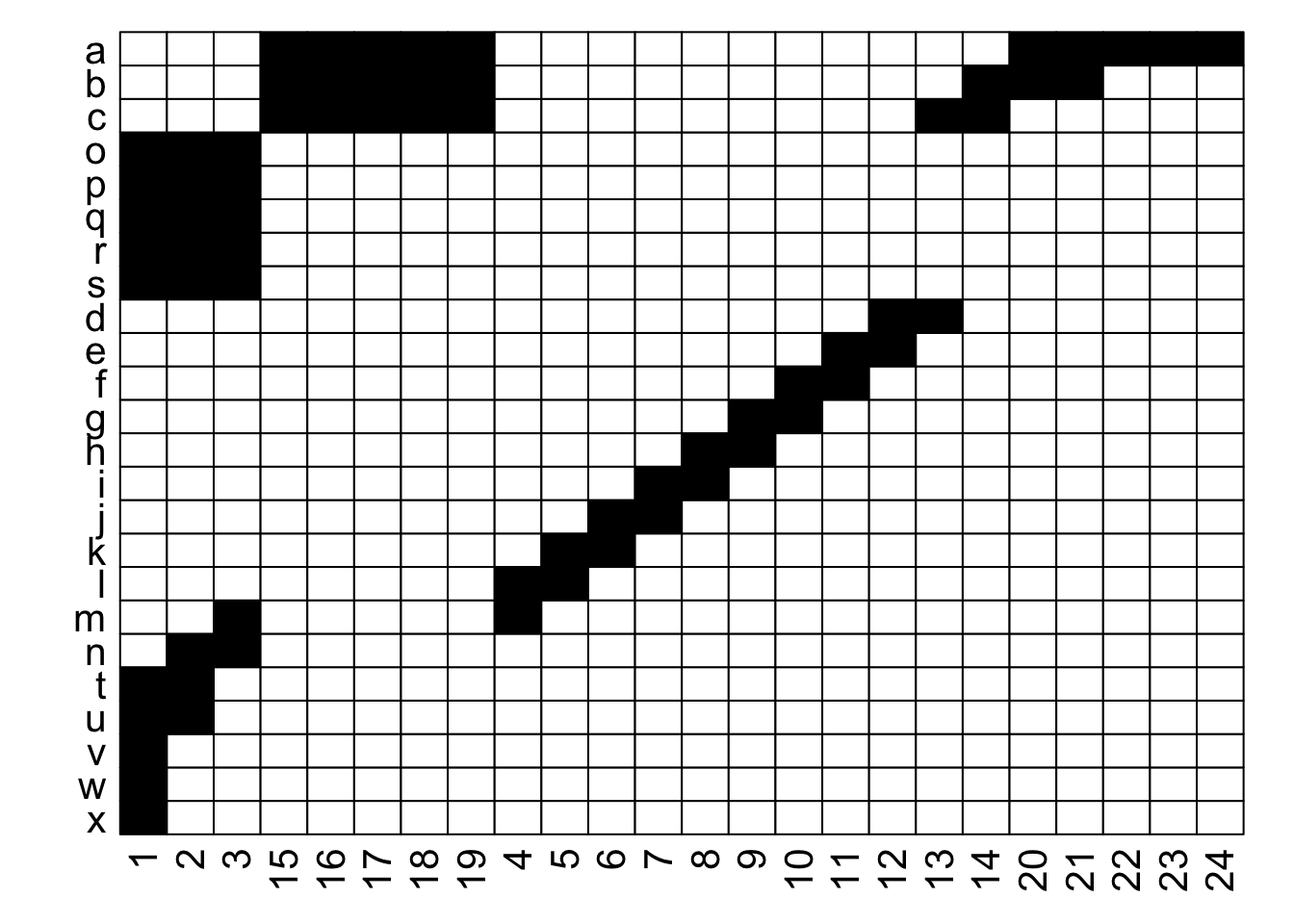
With the row and column labels, you can confirm that the integrity of each interaction is maintained through both of these depictions.
For example, row \(j\) interacts with column 7 in both depictions, and you could hypothetically go through and confirm that for each of the 69 unique interactions in this made-up example (if you were really bored, that is).
To get more detailed without having to go interaction-by-interaction, row \(a\) interacts with columns 15 through 24, and this is easy to confirm in both graphs; it’s just that the column order is different between the two.
Thinking about this, there is a very large number of ways that we could depict the same network…
if \(R\) were the number of rows and \(C\) the number of columns, then we could represent that network in \(R! \times C!\) ways.
For the example above with 24 rows and 24 columns, that is 24! \(\times\) 24!, or more than 3 \(\times\) \(10^{47}\).
In other words, an unfathomably gigantic number of ways.
Put another way, for a 100 \(\times\) 100 network, this value is too large for R to calculate.
With so many potential options, we would ideally like to have a way to standardize how we depict a network in terms of the arrangement of the rows and columns. Thankfully, there is a clear option in this regard (at least when it comes to bipartite networks): we sort the rows and the columns of the matrix by the degree or number of connections that each node has. We sort such that the most-generalist (highest degree) row is at the top, and the most-generalist column is at the left. This depiction maximizes our ability to detect nestedness in our networks (more on that in the next section), and some researchers refer to this arrangement as “packing” a matrix.
When visualizing bipartite networks as matrices, an easy option is to use the visweb function in the bipartite library for R.
visweb includes options for how you display a network.
If your network were called “myweb”, you could call the below to plot the rows and columns in the order they are in the dataset (i.e. no rearrangement):
visweb(myweb, type = "none")
If you want to standardize (order the rows and columns) by the total count of interactions for a particular taxon, you can instead use the bipartite default:
visweb(myweb, type = "nested")
Unfortunately, the bipartite default is not really the ideal way to see nestedness, which is instead to sort by degree or number of links per node (not total number of observed interactions). Because of this, some researchers in the bipartite network realm strongly prefer to order by degree instead of interaction count. To do that, you’ll have to code it yourself. It’s really not hard; some example code is below (and for aficionados of concise code, it would be straightforward to collapse this down into three lines of code).
rows = rowSums(mat>0) # calculate plant degrees
cols = colSums(mat>0) # calculate pollinator degree
roworder = order(rows, decreasing = TRUE) # order plants by degree
colorder = order(cols, decreasing = TRUE) # order pollinators by degree
mat = mat[roworder, colorder] # re-order rows and cols in matrix
To display this, you would have to run this code and then plot with no arrangement:
visweb(myweb, type = "none")
Finally, visweb includes a third option, “diagonal” arrangement, which maximizes the number of interactions occurring along the diagonal of the bipartite matrix.
While a non-standard way to depict matrices, it is helpful for seeing modularity (more on that just below) or compartments in the matrix.
You can do that via this command:
visweb(myweb, type = "diagonal")
Exercise 3
Use the medgarden.csv data you put into matrix form, above
- plot via
visweb:- with
type = "none" - with
type = "nested" - with
type = "diagonal"
- with
- re-order the matrix by plant and pollinator degree using the code included above (or your own variant if you prefer)
- re-plot with
type = "none"; the newly packed data should closely resemble thetype = "nested"network
Metrics of structure
A useful summary of network metrics and their effect on network robustness to species extinctions can be found in this TedEd video: Valdovinos Ted Ed video
Connectance
Connectance measures the proportion of potential interactions that are realized in the network (i.e., the number of different interactions observed as a fraction of the total number of interactions that could possibly occur).
Thus, connectance ranges between 0 (no connections between any species) and 1 (every species interacts with every other species).
In unipartite networks, connectance is calculated by dividing the number of realized interactions (or links connecting species) \(L\) by the square of the number of nodes \(S\) in the network, which represents the total number of interactions if all species were fully connected to one another, including themselves.
So, \(C=L/S^2\).
However, in a bipartite network, nodes from different sets cannot interact.
Which should be the expression for connectance in a bipartite network?
Exercise 4
The denominator of the connectance formula represents the total number of possible interactions in the network, if all species were fully connected to one another. What is the total number of potential interactions in a bipartite network such as a plant-pollinator one?
Exercise 5
Calculate the connectance of the bipartite network graph from Exercise 1 using the formula you derived in Exercise 2.
Nestedness
In a nested network, the interactions of the more specialized species are subsets of the interactions of the more generalized species. Another way to define nestedness is by saying that generalists tend to interact with both generalists and specialists while specialists tend to interact with mostly generalists. Note that the concept of specialist species in a network context is best interpreted as realized interactions and not necessarily as “true specialist” in the evolutionary sense. One particular species can be recorded as specialist (i.e., with only one interaction) in a particular day/week/season but then be recorded as a generalist in the next day/week/season.
Exercise 6
Given the two example networks below, which do you consider to have higher nestedness and why?
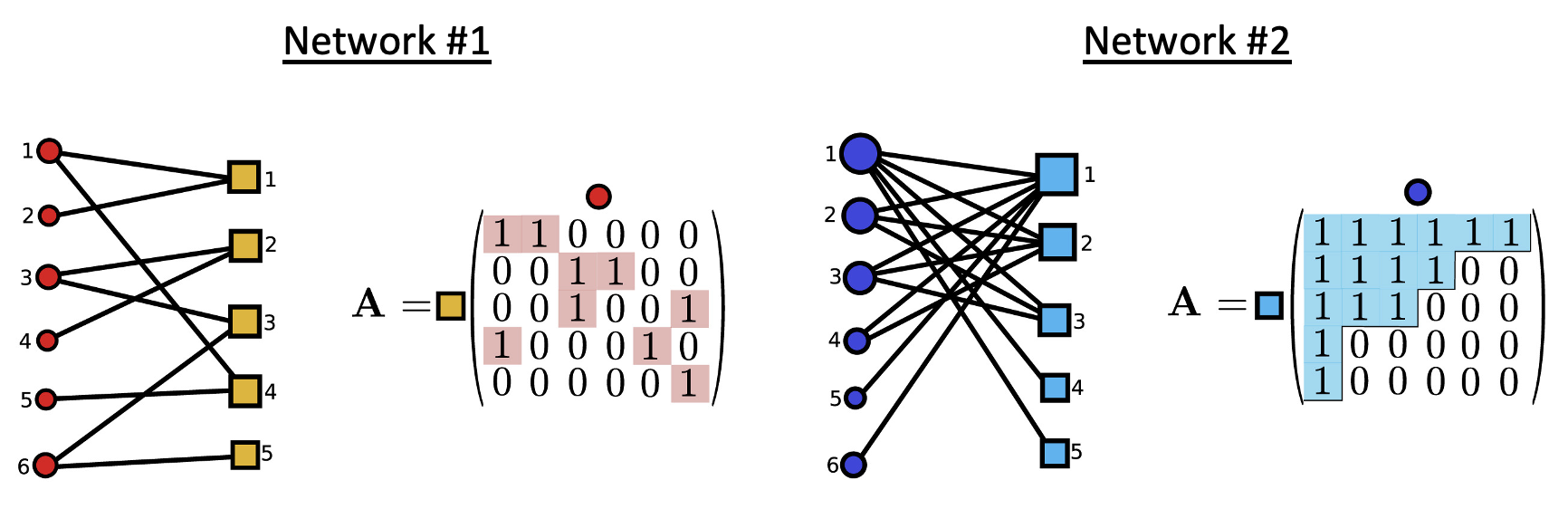
Modularity
A network is said to have high modularity when its interactions are compartmentalized into modules, whose species interact more among themselves than with species belonging to other modules.
Exercise 7
Given the two example networks of Exercise 4, which do you consider to have higher modularity and why?
Calculating metrics
We can calculate network metrics in empirical networks in a relatively straightforward way using the bipartite package for R.
The networklevel() function calculates a huge number of different network metrics. This is not a function to use to spit out a zillion metrics and cherry-pick which ones look best—you will instead want to figure out a priori which metrics you are most interested in, and calculate only those.
For the “Safariland” plant-pollinator network dataset that comes included in the bipartite package, we can calculate nestedness with the NODF metric (there are many other ways to calculate nestedness):
networklevel(Safariland,
index = "NODF")
## NODF
## 24.5478
Easy! We can do the same thing for modularity (note: modularity can take some time to calculate, especially on older / slower computers):
networklevel(Safariland,
index = "modularity")
## modularity Q
## 0.4301558
Exercise 8
Use the medgarden.csv data you put into matrix form, above. Calculate:
\(H_2'\)(network-level specialization); innetworklevel, useindex = "H2"- connectance
Relationships among metrics
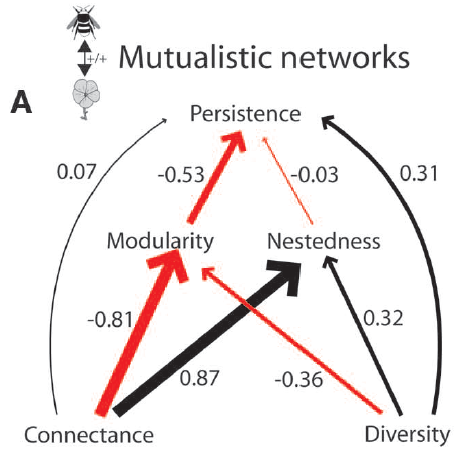
When analyzing the structure of a specific network and especially when comparing the structure of several networks, for example across a latitudinal or altitudinal gradient, you must keep in mind that all these metrics correlate, some positively others negatively. The best known of those relationships is the negative correlation between network richness (i.e., number of species) and connectance, which is shown in this image below taken from Thebault & Fontaine 2010 (Science), where species richness is labeled as “network size” and the black dots are mutualistic networks while the red dots are plant-herbivore bipartite networks.
Exercise 9
Given the mathematical formula of connectance, \(C = L/(P \cdot A)\), how would you explain this well-known negative relationship between species richness, \(S = P + A\), and connectance?
Other known relationships include the positive correlation between connectance and nestedness, the negative correlation between connectance and modularity, the positive correlation between species richness and nestedness, and the negative relationship between species richness and modularity.
Understanding these relationships among network metrics is crucial when analyzing variations across environmental or perturbation gradients in network structure. For instance, if you are investigating how urbanization impacts the network structure of plant-pollinator communities and observe a significant negative impact of urbanization on species richness, caution is needed when comparing other network metrics across the urbanization gradient. This is due to the established relationship between species richness and various network metrics, which could potentially obscure the effect of urbanization by influencing connectance and modularity positively and nestedness negatively. That is, because decreased species richness increases connectance and modularity and decreases nestedness you may infer that it was urbanization which caused those effects on network structure but most likely it is the confounding effect of decreased species richness.
In the past, we all used \(z\)-scores to compare network metrics across networks, but there has been recent criticism to using z-scores for that purpose (Song et al 2017, Journal of Animal Ecology).
Song et al proposed a new nestedness metric, \(NODFc\), which can be calculated using the R package “maxnodf” (Hoeppke & Simmons 2021, Methods in Ecology and Evolution) to compare nestedness across networks.
Other researchers have used statistical analyses such as generalized linear mixed models to disentangle the effect of a specific treatment from species richness on other network metrics.
Covering these recent alternatives and the criticism of using \(z\)-scores is beyond the scope of this course but it is important that you are aware of these recent developments and, most importantly, that you are aware of the known relationships between network metrics so you consider them when making inferences based on your network analyses.
Null models
In some situations, it is helpful to know if an empirical network exhibits a value of some network metric that is greater than you would expect by chance alone. Nestedness is a good example, because we might actually expect networks to display some level of nestedness just because of some of the basic facts of how they are set up. Most communities display a very skewed distribution of abundances, with one or just a few species having very high abundance, and then a lot of species with low abundances. If we have such an abundance distribution for both guilds (e.g. plant and pollinator species), and plants and pollinators are interacting with one another purely at random, we would expect that rare pollinator species would be most likely to interact with common plant species, and that rare plant species would be most likely visited by common pollinators. This is especially true if we are sampling the network on a per-area basis (in which we would log much more observation time on the most common plants). Taken together, the elements of this scenario—which with the exception of the random interactions, is pretty much the case in most plant-pollinator networks—would lead to a very nested pattern.
Given that, we might ask if a network is more nested than we would expect it to be relative to chance alone. We can do this with null model simulations. What exactly is a null model? It’s a concept that has been surprisingly difficult to pin down, but the definition provided in the book “Null Models in Ecology” by Nick Gotelli & Gary Graves (1996, Smithsonian Institution Press, Washington, D.C.) is a helpful one:
“A null model is a pattern-generating model that is based on randomization of ecological data or random sampling from a known or imagined distribution. The null model is designed with respect to some ecological or evolutionary process of interest. Certain elements of the data are held constant, and others are allowed to vary stochastically to create new assemblage patterns. The randomization is designed to produce a pattern that would be expected in the absence of a particular ecological mechanism.”
If we were asking if a network is more nested than we would expect with chance alone, one way to frame that is to say that we don’t think interactions are happening randomly between plants and pollinators. Instead, plants and pollinators have traits that structure their interactions; pollinators draw down resource levels in flowers that then affect the preferences of other pollinators, etc. But, we can create a null model where we assume interactions are happening randomly, repeat that random interaction assignment many times, and then assess if our actual data are different (e.g., more or less nested) than we would expect based on random interactions. The basic statistical idea here is a permutation test, for those of you familiar with that concept.
Alternatives
But that sounds pretty complicated (and to be honest, it is not the most straightforward thing ever)—so how do we actually implement null models in practice? Luckily, the bipartite package has built-in algorithms to create null models (and there are other R packages that do as well, notably vegan), so you don’t have to code these by hand (phew!). But because there are different kinds of null models, it is critically important to understand what is going on “under the hood” of the algorithm so that you can apply the right null model to your analysis.
Simplest null model
Let’s start by thinking about the simplest possible way we could create a null model. We want to assume that interactions are happening at random.
Perhaps a first-pass way of doing this would be to say something along the lines of “well we have our plant species and our pollinator species,
i.e. our bipartite matrix, and we recorded a total of \(N\) interactions in our empirical data… all we have to do is randomly assign each interaction to one cell in our bipartite matrix, and we’ll end up with a randomized network”.
That would be one way to do it, but it has some pretty major downsides.
One downside is that when you repeat that procedure, especially if your \(N\) is relatively small, you are likely to have one or more species that have no interactions and thus would drop out of the network.
Because some network metrics are sensitive (sometimes very sensitive) to network size / species richness, that’s definitely not ideal. You could get around that downside, perhaps by first assigning one interaction to each row (a random column in that row), and then assessing if all columns have an interaction, and for any that are missing, assigning a random interaction to that column.
Then you could assign all of the “leftover” interactions randomly as described above.
Constant link number
Making sure the species richness stays constant is an important improvement over the first-pass method, but the sketch of a null model described above still ultimately has some problems.
One key reason is that while the number of total interactions is maintained, the sketch of the algorithm described above does not maintain the same number of links in the network. Given a wide-open matrix in which to assign interactions, in particular such an algorithm will typically generate many more links than we would see in an empirical dataset, and that is also definitely not ideal.
A “second-pass” null model would maintain the same number of interactions (as we suggested in the “first-pass” model), but would also maintain the number of links (and therefore hold connectance constant).
This is what the shuffle.web algorithm in the bipartite package does.
This is an algorithm that has been used in some papers, e.g. Fortuna, M. A., and J. Bascompte. 2006. Habitat loss and the structure of plant-animal mutualistic networks. Ecology Letters 9: 281-286.
Constant degree
Still, the shuffle.web null model algorithm is not widely used these days.
A major reason is that (again) some plants, and some pollinators, are much more common, and some are rare.
And that skewed abundance distribution could be a big driver of any nestedness we see in a system (as well as potentially other network metrics).
To account for that, we can instead implement what we might call a “third-pass” algorithm that accounts for the empirically-observed number of interactions for each species, and holds those “marginal totals” constant.
In practice, this would be straightforward to do for just one of the guilds in our network—let’s say we do it for plants. We can take the total number of interactions for each plant species, and assign them randomly across the pollinators in the network. Easy-peasy.
The problem is that we are trying to do this also at the same time for pollinators, and that is a lot trickier!
Again, luckily we don’t have to code this by hand.
This null model is implemented in the r2dtable function in bipartite.
Constant link number and degree
Taking our exploration of null models yet another step further, r2dtable is very helpful in terms of accounting for the number of interactions that each species has.
But accounting just for that does not necessarily give us the same number of links (or put another way, connectance) displayed by our data, as we described above.
So a “fourth-pass” algorithm would hold multiple components constant relative to the empirical data:
- the total number of interactions in the whole network;
- the degree of each plant and pollinator species; and
- the number of links across the entire network / connectance.
This is (at least theoretically) implemented in the
swap.webfunction inbipartiteand is a very commonly-used null model. This approach was first implemented in: Miklós, I. and Podani, J. (2004) Randomization of presence-absence matrices: comments and new algorithms. Ecology 85, 86–92.
There are other approaches as well, for example the vaznull function uses an approach proposed by Diego Vázquez et al. in 2007 (Oikos 116: 1120-1127).
This algorithm weights the probability of selecting a cell (interaction) in the matrix by the abundance (number of empirically observed interactions) of both the plant and the pollinator.
While similar to the r2dtable algorithm in that regard, it does not hold the row and column sums to be absolutely constant, even though they are weighted by interaction abundance.
The vaznull algorithm is also supposed to maintain equal or close-to-equal connectance, like swapweb.
Comparing null models
Ultimately, however, it’s important to understand that every null model has drawbacks. In particular, more constrained is not always better.
The more things that are held constant, the fewer potential randomizations there are that can be done that meet all of the criteria.
For some unusually structured networks (especially for small networks) the number of possible permutations becomes very small for highly constrained algorithms like swap.web.
Moreover, the swap.web and vaznull approaches have been criticized for biasing some “swaps” of interactions (i.e. some swaps are more likely than others, when they shouldn’t be).
There is to our knowledge no “perfect” null model implementation but it’s also good to know that network null models are also implemented in other packages, notably there are >25 null model algorithms implemented in the vegan package.
To learn more, check out the documentation of the commsim function: ?vegan::commsimm.
Graphical implementation
Let’s delve into how to use these algorithms in practice, starting by graphically implementing a null model analysis (we discuss how to calculate a \(p\)-value for this procedure below).
For this graphical analysis, we’ll focus on NODF (again, a metric of nestedness) in the “Safariland” plant-pollinator network dataset that is included in the bipartite package (code below altered slightly from Carsten Dormann’s bipartite vignette). We will use the swap.web algorithm and create 999 null networks to compare with the empirical “Safariland” dataset.
We will plot the NODF value of the empirical dataset as a red vertical line, and display the distribution of the null networks with a density plot (we could just as easily display it as a histogram as an alternative, code included but commented out). Here is the code:
# Load the 'Safariland' data from the bipartite package
data(Safariland)
Iobs <- networklevel(Safariland, index = "NODF")[[1]]
nulls <- nullmodel(web = Safariland,
N = 999,
method = 'swap.web') # can take a while...
Inulls <- sapply(nulls,
function(x){nestednodf(x)$statistic[3]})
plot(
density(Inulls),
xlim = c(0, 100),
lwd = 2,
main = "NODF"
)
# plot(hist(Inulls), xlim=c(0, 100), lwd=2, main="NODF") # histogram
abline(v = Iobs,
col = "red",
lwd = 2)
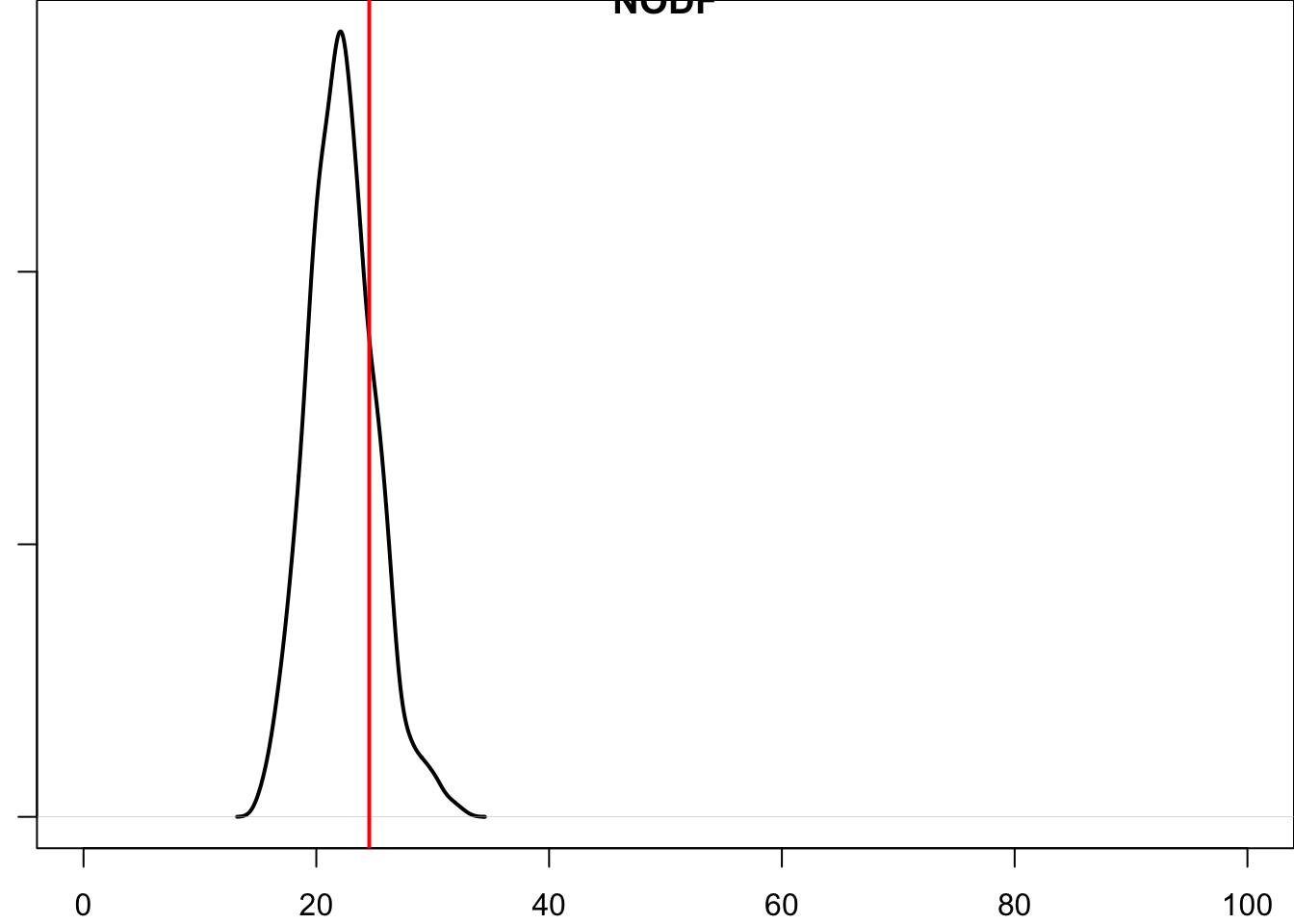
What we see is that the NODF (nestedness) value of the empirical dataset—the red line—is somewhere in the middle of the distribution of the null-model NODF scores. That is, our empirical value would likely not be considered either more or less nested than chance alone.
Checking results
Before we get to \(p\)-values, it is always worth checking if the null model we are using actually has the properties that we want.
Relative to the empirical network, the swap.web algorithm is supposed to: 1) maintain the connectance; and 2) maintain the row and column sums.
Let’s check that it is actually doing that. We’ll calculate the mean and standard deviation of connectance across all 999 networks;
we should be getting an exact or very close to exact match with our empirical connectance, and a standard deviation that is either zero (meaning all of the null networks have the exact same connectance) or very very small.
We can then compare the row and column sums.
We’ll start with connectance:
# calculate connectance across the null networks
Cnulls <- sapply(nulls,
function(x){
networklevel(x, index = "connectance")[1]
})
Cempirical <- networklevel(Safariland, index = "connectance")[1]
SDnulls <- sd(Cnulls)
## mean connectance of null networks = 0.1604938
## connectance of empirical network = 0.1604938
## standard deviation of null networks = 0
Looks great: connectance is exactly the same between the two, and the standard deviation in connectance in the null networks is zero, meaning that each and every null network has the exact same connectance as our empirical network.
Still, it is worth trying this, because sometimes—even in recent versions of bipartite—we have had the experience where these null models do not perform exactly as expected.
In those cases, usually if we start a new R session and re-try, it works… but again, it is definitely worth checking.
Now let’s check the species degrees (row and column sums). This one is just a little trickier, because there is one value for each species in the network, not just one numeric value for the entire network (as there was with connectance). To account for that, we will put the values—for both the row and the column sums—into a data frame, with rows as species and a column for each of the empirical data and the means of the null models. A nice way to check this formally is then to subtract those two columns; if they are exactly the same (as they should be), then the difference for each value would be zero.
We will do the procedure for both the pollinators and the plants, but we will just display the results in tabular form for the 9 plant species in the “Safariland” dataset to save space.
# calculate row sums across the null networks
Rsums.nulls <- sapply(nulls,
function(x){ rowSums(x) })
# this returns a 9 x 999 matrix, with one column for each null model
# now take the mean across all of those row sums:
Rsums.mean <- apply(
Rsums.nulls,
MARGIN = 1,
FUN = function(x){ mean(x) })
# we'll put this into a data frame along with the empirical row sums:
comper = data.frame(empirical = rowSums(Safariland),
null = Rsums.mean)
# we will check that out in just a second, but first we'll add the col sums:
Csums.nulls <- sapply(nulls,
function(x){ colSums(x)})
Csums.mean <- apply(
Csums.nulls,
MARGIN = 1,
FUN = function(x){ mean(x) })
comper2 = data.frame(empirical = colSums(Safariland),
null = Csums.mean)
# bind row & col sum dataframes together:
comper = rbind(comper, comper2)
# subtract null values from empirical values
# (all should be zero if algorithm performing correctly)
comper$difference = comper$empirical - comper$null
# display
kable(comper[1:9, ], row.names = TRUE) %>%
kable_styling(
full_width = FALSE,
position = "left",
bootstrap_options = "condensed"
)
| empirical | null | difference | |
|---|---|---|---|
| Aristotelia chilensis | 790 | 790 | 0 |
| Alstroemeria aurea | 208 | 208 | 0 |
| Schinus patagonicus | 15 | 15 | 0 |
| Berberis darwinii | 72 | 72 | 0 |
| Rosa eglanteria | 15 | 15 | 0 |
| Cynanchum diemii | 20 | 20 | 0 |
| Ribes magellanicum | 5 | 5 | 0 |
| Mutisia decurrens | 1 | 1 | 0 |
| Calceolaria crenatiflora | 4 | 4 | 0 |
Looks great—all of the row sums (plant degrees) are the same between the null models and the empirical network.
Again, the code above included all of the column sums (pollinator degrees), as well as a column for difference between empirical row/column sums and mean null model row/col sums.
We could easily assess if there were any departures from zero with this line of code: which(comper$difference!=0).
If it returns integer(0) you know that they match perfectly (in this case, they do).
Of course, we didn’t check out the standard deviations here, so there is a small chance that there is some variation across the null models (but a pretty tiny chance indeed, given that we see integers for all of the mean values…) but that is something that would be easy to add to the code above if you were interested.
Bringing this back full circle, that means that the swap.web algorithm is doing what we expected relative to the empirical data:
- maintaining the same connectance
- maintaining the same row and column sums
while we didn’t do an explicit check to see if the total number of interactions is the same between the two, we couldn’t maintain the same row and column sums and also have a different total number of interactions, so we are safe there as well.
p-values
Our first pass at the null model analysis above was graphical.
We can formalize this test in a very straightforward way, calculating a \(p\)-value by assessing the rank of the empirical value relative to the nulls.
Let’s imagine a case in which the empirical value was more-nested than almost all of the nulls.
If we were to generate 99 nulls, and out of the 100 total networks we were assessing (the 99 nulls + the 1 empirical network), the empirical network was the 5th-most nested (i.e. 4 null models were more nested), then the \(p\)-value would be exactly 0.05 (5 out of 100).
One way of conceptualizing that is that if the empirical value was part of the same distribution as our null models, we could assign it a rank in that distribution at random.
And there would only be a 5% chance ($p$ = 0.05) that the rank would be 5th or more extreme (4th, 3rd, 2nd, or 1st).
Similarly, if the empirical network were the most-nested of all, the \(p\)-value would be 0.01 (1 out of 100).
Two lessons from that:
first, it makes the \(p\)-value calculations slightly easier if you generate {some power of 10 minus 1} null models, e.g. 99 or 999 or 9,999 null models.
Still, that is not strictly required.
And second, the more null models you calculate, the greater the precision you have in your \(p\)-value. The examples above were for 99 null models;
if you were to use 9,999 nulls and your empirical network were the top-ranked one, the \(p\)-value would be 0.0001 (1 in 10,000).
The caveat there is that the more null models you calculate, the longer it takes.
Typically if you’re after assessing statistical significance in the traditional sense, you will want to use more than 99 null models, as that is pretty coarse, especially since you can have slight variations in the \(p\)-value if you re-run your null models.
Still, once you get to 999 you should (usually) know if the \(p\)-value is less than the standard \(\alpha\) value of 0.05. If you have a borderline value, you might want to amp up the resolution by running more null models.
It’s also worth noting that the \(p\)-values as described above are for a one-tailed test.
For example, if you had the a priori hypothesis that your empirical network was more nested than you would expect by chance, then you could assess that with a one-tailed test.
If you wanted to see if your network was either more or less nested than chance alone, for the example with 99 null models, if your empirical data were either the most or the least nested, there is a 1 in 100 chance of either of those situations happening.
So you would need to multiply the \(p\)-value by 2 to compensate:
there is a 2 in 100 chance of either occurring, so the \(p\)-value for either situation would be not 0.01, but 0.02.
p-value calculation
With all of that in place, we can write code to calculate the (two-tailed) \(p\)-value.
A few things to note:
- we use
length(which())to assess rank, by seeing how many null values are more-extreme than our empirical value - to properly assess the rank of the empirical data, we add 1 to the result of
length(which())- if there were say 11 null values that were smaller, the rank of the empirical data would then be 12th (not 11th)
- adding 1 also corrects the situation where the empirical value is the most-extreme, i.e. zero null values would be less than the empirical value. In that case, we want the p-value to be (say) 0.001 or 0.0001, not 0.
- because this is a two-tailed test, we assess if the rank of the empirical value is greater than or less than the mean of the null distribution (using
minbelow) - again because of the two-tailed nature of the test, we multiply the value by 2 at the end
# two-tailed p-value for permutation test with null models
pval = (min(length(which(Inulls > Iobs)),
length(which(Iobs > Inulls)) + 1) /
length(c(Iobs, Inulls))) * 2
## p = 0.36
In this case, we can see that the \(p\)-value is 0.36, i.e. the Safariland network is not significantly nested relative to chance.
Take-home
Together these examples point to a few take-home messages:
- the precise null model you use for your analysis matters—different null models can give you completely different results
- in general, a good default is to use a more conservative null model algorithm, i.e. one that holds constant more features of the empirical network
- but be careful especially with small networks that your null models are not too constrained to generate substantive enough variation
- always check your null models to make sure they are performing as expected
- use a two-tailed
\(p\)-value as a default, unless you have laid out an a priori hypothesis that includes directionality (e.g., “I hypothesize that this network will be less-nested than chance alone would predict”)
Exercise 10
Analyze NODF for the “Safariland” dataset using the r2dtable null model,
- graphically and
- by calculating the (two-tailed)
\(p\)-value. You should get a qualitatively different result relative to usingswap.web. Describe where the empirical value falls out relative to the null models.
Bonus exercise
Using the information above on the correlation among network metrics, as well as descriptions of the null models, offer an interpretation as to why the two null models yield qualitatively different results.
Double bonus exercise
Try one of the null models implemented in vegan, in particular quasiswap_count.
Here is some code that should help you; the syntax is different for the vegan implementation relative to bipartite and in addition vegan returns the null models not as a list, but instead as a 3-dimensional array.
The latter means you need to take a slightly different approach when calculating NODF (or any other metric) across the null models.
## Alternative: use vegan::nullmodel rather than bipartite
# install.packages('vegan', dependencies = TRUE)
library(vegan)
# Require first setting up a null model, then separately simulating it
n.vegan <- vegan::nullmodel(Safariland, "quasiswap_count") #setup
nulls.vegan <- simulate(n.vegan, nsim = 999) #simulation
# The vegan `simulate` method returns a 3-dimensional numeric array
# so need to modify the code used for the bipartite nulls
# use `apply` rather than `sapply` with MARGIN = 3
Inulls.vegan <- apply(nulls.vegan,
MARGIN = 3,
FUN = function(x){nestednodf(x)$statistic[3]})
If you go for the “double bonus” round, you should get again a qualitatively different result relative to swap.web.
This is somewhat curious as the two methods are supposed to be very similar….
Structure & Stability
Networks are useful descriptors of community structure but also they matter for the stability of communities. Researcher have investigated the effect of networks structure on community dynamics including their stability since Robert May’s pioneer work in 1972 showing mathematically that increased levels of complexity decreases stability of communities. Some concepts of stability you will find in the network literature include:
- Local stability: A system is locally stable if it returns to its original state after being slightly disturbed. Mathematically, local stability is often analyzed through the concept of stability analysis, which involves examining the behavior of a system near an equilibrium point. One common method used to analyze local stability is through linearization, where the system’s dynamics are approximated by a linear model around the equilibrium point. This is the concept used by Robert May’s work and because its simplicity, has been used by many in the field. However it has important limitations, including the assumption of a local equilibrium, the inability of evaluating any but small perturbations, and the assumption of linear dynamics at equilibrium.
- Resilience: Time to return to a local equilibrium after slightly perturbing the system away from it.
- Structural Stability: In local stability analysis the perturbations act on state variables, limiting the analysis to changes in species abundances only. Conversely, one can study other perturbations using structural stability analysis. A system is considered to be structurally stable if any smooth change in the model itself or in the value of its parameters does not change its dynamic behavior (e.g., existence of equilibrium points, limit cycles, chaos, etc).
- Feasibility: All the constituent species from the community attain positive abundances at equilibrium.
- Species persistence: Typically used in studies of computer simulations, defined as the fraction of initial species that persists until the end of the simulations.
- Robustness against species extinctions: Typically defined in studies of computer simulations as the resistance of a network to loose more species (as secondary extinctions) as result of primary extinctions, which are typically simulated as the removal of species from the network.
We will elaborate more on the effect of network structure on network dynamics and stability in day 3.
Session Info
sessionInfo()
## R version 4.4.3 (2025-02-28)
## Platform: aarch64-apple-darwin20
## Running under: macOS Sequoia 15.6.1
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib; LAPACK version 3.12.0
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## time zone: America/Denver
## tzcode source: internal
##
## attached base packages:
## [1] grid stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] bipartite_2.20 sna_2.7-2 network_1.18.2
## [4] statnet.common_4.9.0 kableExtra_1.4.0 lubridate_1.9.3
## [7] forcats_1.0.0 stringr_1.5.1 dplyr_1.1.4
## [10] purrr_1.0.2 readr_2.1.5 tidyr_1.3.1
## [13] tibble_3.2.1 ggplot2_3.5.1 tidyverse_2.0.0
## [16] gridGraphics_0.5-1 rmarkdown_2.28 viridis_0.6.5
## [19] viridisLite_0.4.2 vegan_2.6-8 lattice_0.22-6
## [22] permute_0.9-7 evaluate_0.24.0 knitr_1.48
## [25] igraph_2.0.3
##
## loaded via a namespace (and not attached):
## [1] dotCall64_1.1-1 spam_2.10-0 gtable_0.3.5 xfun_0.47
## [5] bslib_0.7.0 tzdb_0.4.0 vctrs_0.6.5 tools_4.4.3
## [9] generics_0.1.3 parallel_4.4.3 fansi_1.0.6 highr_0.11
## [13] cluster_2.1.8 pkgconfig_2.0.3 Matrix_1.7-2 lifecycle_1.0.4
## [17] compiler_4.4.3 fields_16.2 munsell_0.5.1 maps_3.4.2
## [21] htmltools_0.5.8.1 sass_0.4.9 yaml_2.3.8 pillar_1.9.0
## [25] jquerylib_0.1.4 MASS_7.3-64 cachem_1.0.8 nlme_3.1-167
## [29] tidyselect_1.2.1 digest_0.6.35 stringi_1.8.4 bookdown_0.39
## [33] splines_4.4.3 fastmap_1.1.1 colorspace_2.1-0 cli_3.6.2
## [37] magrittr_2.0.3 utf8_1.2.4 withr_3.0.0 scales_1.3.0
## [41] timechange_0.3.0 gridExtra_2.3 blogdown_1.19 hms_1.1.3
## [45] coda_0.19-4.1 mgcv_1.9-1 rlang_1.1.3 Rcpp_1.0.13
## [49] glue_1.7.0 xml2_1.3.6 svglite_2.1.3 rstudioapi_0.16.0
## [53] jsonlite_1.8.9 R6_2.5.1 systemfonts_1.0.6